Natural Language Processing Tutorial
Introduction
This will serve as an introduction to natural language processing. I adapted it from slides for a recent talk at Boston Python.
We will go from tokenization to feature extraction to creating a model using a machine learning algorithm. The goal is to provide a reasonable baseline on top of which more complex natural language processing can be done, and provide a good introduction to the material.
The examples in this code are done in R, but are easily translatable to other languages. You can get the source of the post from github
Training set example
Let’s say that I wanted to give a survey today and ask the following question:
Why do you want to learn about machine learning?
The responses might look like this:
## 1 I like solving interesting problems.
## 2 What is machine learning?
## 3 I'm not sure.
## 4 Machien lerning predicts eveyrthing.
Let’s say that the survey also asks people to rate their interest on a scale of 0 to 2.
We would now have text and associated scores:

First steps
- Computers can’t directly understand text like humans can.
- Humans automatically break down sentences into units of meaning.
- In this case, we have to first explicitly show the computer how to do this, in a process called tokenization.
- After tokenization, we can convert the tokens into a matrix (bag of words model).
- Once we have a matrix, we can a machine learning algorithm to train a model and predict scores.
What is the algorithm doing?
- The algorithm is going to be taking in a lot of numerical values, along with the scores that are associated with these values.
- We will extract the numerical values from the text
- For example, number of times the word plane appears in a piece of text is a feature.
- The values (features) are derived from the input text, and aggreggated on a per-text basis into feature vectors.
- Multiple feature vectors are generally placed together into a feature matrix, where each row represents a piece of text.
- The algorithm will discover which of these features is relevant, and which are not.
- The relevance is determined by whether or not the features differentiate a high scoring essay from a low scoring one.
- So, we want to feed it features that are specific (they measure as few things as possible) and relevant.
Tokenization
Let’s tokenize the first survey response:
## [1] "I" "like" "solving" "interesting" "problems"
In this very simple case, we have just made each word a token (similar to string.split(’ ‘)).
Tokenization where n-grams are extracted is also useful. N-grams are sequences of words. So a 2-gram would be two words together. This allows the bag of words model to have some information about word ordering.
Bag of words model
- The bag of words model is a common way to represent documents in matrix form.
- We construct an nxt document-term matrix, where n is the number of documents, and t is the number of unique terms.
- Each column represents a unique term, and each cell i,j represents how many of term j are in document i.
- We are using a simple term frequency bag of words. Other techniques, such as term frequency - inverse document frequency (tf-idf) would have something other than just counts in the cells.
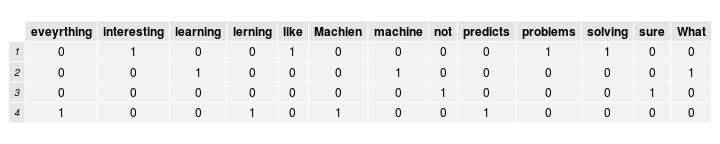
Bag of words overview
- Ordering of words within a document is not taken into account in the basic bag of words model.
- Once we have our document-term matrix, we can use machine learning techniques.
- I have outlined a very simple framework, but it can easily be built on and extended.
- The bag of words is a foundational block for a lot of more advanced techniques.
- What we are doing is extracting potentially relevant information in a manner the computer can utilize (ie numbers)
Minimizing distances between vectors
- We want to minimize the distance between two similar feature vectors.
- For example, the below text fragments are substantially similar:
- Bill wanted to grow up and be a Doctor.
- bill wnted to gorw up and a be a doctor!
- However, the simple tokenization we outlined above will not catch this.
- Spell correction using aspell or Peter Norvig’s method.
- Lowercase input strings.
- We minimize distance because we want the same response to get the same score from our algorithm.
Preserving information
- It is important to preserve as much of the input information as we can.
- When we start to spell correct or lowercase strings, we lose information.
- We may be lowercasing the proper name Bill to the word bill.
- If we are scoring an essay, and spelling is an important criteria, we don’t want to lose that.
Old features:
 New features with lowercasing and spell correction:
New features with lowercasing and spell correction:

Orthogonality
- As we saw in the slide before, we want to generate as much new information as possible while preserving existing information.
- This will have us generate multiple feature sets. All of the feature sets will eventually be collapsed into one matrix and fed into the algorithm.
- Recommend having one feature set with original input text.
- Can measure orthogonality by taking vector distance or vector similarity between each document vector.
- Need to reformat document vectors to contain all terms.
Cosine similarities:
## [1] 1.0000 0.6667 1.0000 0.2500
Mean similarity:
## [1] 0.7292
Meta-features
- We may also wish to extract higher-level features, such as number of spelling errors, number of grammar errors, etc.
- Can add meta-features to the bag of words matrix.
- Meta-features preserve information.
- If we are lowercasing everything, a “number of spelling errors” feature will capture some of the original information.
- Can also extract and condense information.
- Several columns with capitalized words will contain a lot of word-specific information (including whether or not the word is capitalized), but making a feature “number of capitalizations” will condense all of that information.
- If one of the criteria for whether or not an essay is good is whether or not the student has a synonym for “sun”, a meta-feature could extract all possible synonyms and condense them into a count.
Relevance of Information
- Just like with a human, too much information will swamp an algorithm will irrelevant inputs.
- Similarly, information that is too broad will not help much.
- For example, say a latent trait that gives a student a 2/2 on an essay vs a 0/2 is the presence of a synonym for the word “sun” in the response
- Broad information would be several columns in our matrix that contain synonyms for the word “sun”
- Specific information would be a feature that counts all of the synonyms up
- Our goal is to give the computer as much relevant information as possible. If an item is relevant, more specific is better, but the less specific it is, the more potentially relevant it will be.
Which features are the right features?
- Two simple ways
- Create a machine learning model and measure error
- Do a chi-squared test or a fisher test of significance.
- The tests essentially say “Is feature x significantly different between low and high scoring texts”?
- P-value – the lower the p-value, the more significant the difference is. Generally, a .05 or a .01 is a good threshold for significance.

Finally, some machine learning!
- Now that we have generated our bag of words features and our meta-features, and figured out which ones are good, we can move onto machine learning.
- The goal is to “train” a model that can predict future scores and categories.
- Two broad categories of algorithms: classification and regression (not linear regression!)
- Most regression assumes that you are on a continuous scale.
- Classification is discrete.
- Classification works best if you have less than 5 “score points” (we have 3).
- Should try both, and measure error.
- We also have a lot of choice regarding the algorithm to use.
- In this case, use linear regression
Linear regression
- A simple linear equation is , where y is the target value(score), m is a coefficient, and b is a constant.
- In linear regression, we would do something like .
- Each column in the matrix (feature) has a coefficient.
- When we train the model, we calculate the coefficients.
- Once we have the coefficients, we can predict how future text would score.
Coefficients:
## (Intercept) eveyrthing interesting learning
## coefficients 1 -1 1 -1
Words that are not shown do not have a coefficient (ie they did not have any useful information for scoring).
Predicting scores
- Now that we have our coefficients, and our intercept term, we can construct our equation and predict scores for new text.
- Any new text has to go through the exact same process that we passed our training text through.
- In this case, text will go through the bag of words model. We will skip additional processing to keep it simple.
Let’s use this as our “test” text that we will predict a score for:
## 1 I want to learn to solve interesting problems.

- Note that we have used the exact same features as in the training matrix.
- Without this, our model will not work.
Doing the prediction
We can use our new features to predict a score for our test text.
Our prediction is 2
We derive this by multiplying each column in the matrix by its associated coefficient, then adding those together and adding the intercept.
In this case, the intercept was 1 and the presence of the word interesting added another 1.
Evaluating model accuracy
- A very important question when creating a model and exploring various feature combinations is accuracy.
- In order to measure accuracy, we use a principle called cross-validation.
- Split training data set into n parts randomly (each part is a “fold”, and we call it n-fold cross validation).
- Iterate from 1 to n and predict the scores of parts[n] from all the data in parts[!n].
- Let’s keep it simple, and split into 2 parts non-randomly.
- We will make a model using only the first 2 training matrix rows, and then another model using the next 2.
- Each model will be used to predict the scores of the texts that did not go into the model.
- Why do we do this?
- Measuring accuracy allow us to figure out optimal combinations of strategies.
- Cross validation gives us an unbiased accuracy estimate.
Evaluating model accuracy
First fold:
 Second fold:
Second fold:
 Predictions:
Predictions:
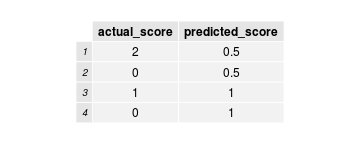
- Predictions are not very accurate due to very limited data.
Quantify error
- Quantify accuracy through one of several methods
- Kappa correlation
- Mean absolute error
- Root mean squared error
- All of them turn error into a single number
- Important to set random seeds when doing most machine learning methods in order to make error meaningful from run to run.
- Our RMSE is 0.9354
- If we tried another method, and the RMSE improved, we would have a reasonable expectation that the method was better.
More advanced features
- Find similarity between documents or terms with latent semantic analysis.
- Model topics with latent dirichlet allocation
- Part of speech tagging
- Stemming/lemmatization
- Synonym detection with wordnet
- Sentiment analysis
- Deep learning
More advanced algorithms
- Support vector machines
- Decision trees
- Random forest
- Gradient boosted trees
- Different algorithms work better in different situations. Try several.
- A framework to measure error is critical before experimenting.
- You can also “blend” the outputs of various algorithms in a process called ensembling.
