Time Based Arbitrage Opportunities in Tick Data
I recently posted an [introduction](http://viksalgorithms.blogspot.com/2012/01 /introduction-to-kaggle-algorithmic.html) to the Kaggle Algorithmic Trading Challenge, which I competed in.
I said that I would post about my experiences, and this is hopefully the first of a series. We were given tick data from the London Stock Exchange(specifically, the FTSE 100) over random time intervals during parts of 37 days. Each data row that we were given corresponded to a liquidity shock event and the surrounding bid/ask prices. Given 50 bid prices and 50 ask prices prior to the liquidity shock event, we had to predict the next 50 bid and ask prices.
I, and others, noticed that there were distinct areas of high volatility in the tick data at certain times of day. Specifically, 10:15, 13:30, and 15:00 (london time) all showed abnormal volatility.
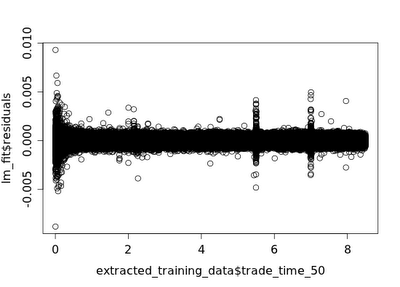 The above chart plots the residuals of a simple linear model that predicts the average of the first five bid and ask prices after the liquidity shock event at t=50 against the time the trade was made. The x-axis(time the trade was made) is in the units of hours after 8:00, so a value of 2 on the x-axis corresponds to 10:00. The residuals of the linear fit indicate how “hard” the values of the bid-ask time series were to predict, which is a proxy for volatility. The below R code generated the plot:
The above chart plots the residuals of a simple linear model that predicts the average of the first five bid and ask prices after the liquidity shock event at t=50 against the time the trade was made. The x-axis(time the trade was made) is in the units of hours after 8:00, so a value of 2 on the x-axis corresponds to 10:00. The residuals of the linear fit indicate how “hard” the values of the bid-ask time series were to predict, which is a proxy for volatility. The below R code generated the plot:
lm_fit<-lm(current_formula,data=cbind(extracted_training_dependent_variable, extracted_training_data))
plot(x=extracted_training_data$trade_time_50,y=lm_fit$residuals) This can also be observed when plotting the normalized standard deviation of the bid series against trade time, although the spike at 10:15 is harder to see:
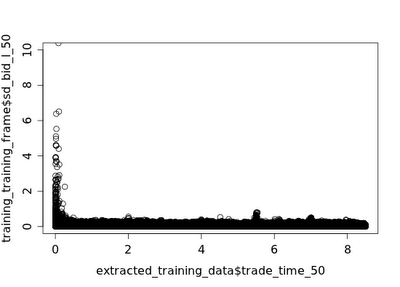 Although the spike in volatility at 13:30 appears to be caused by the opening of the NASDAQ and NYSE, it is unclear what the other two spikes might represent, although other markets may be opening at those times. Specifically, the spikes appear to be caused by other markets/traders valuing the stocks differently, which leads to an opportunity for profit taking.
Although the spike in volatility at 13:30 appears to be caused by the opening of the NASDAQ and NYSE, it is unclear what the other two spikes might represent, although other markets may be opening at those times. Specifically, the spikes appear to be caused by other markets/traders valuing the stocks differently, which leads to an opportunity for profit taking.
Here is a typical series in which a spike occurs:
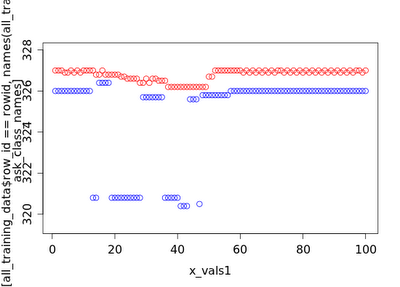 In this series, a liquidity shock occurs when x=50(although there are several shocks prior to this). The whole sequence from x=1 to x=50 takes place over 13 seconds, and each x value is a distinct trade or quote event. The red points are ask prices, and the blue points are bid prices. As you can see, there appears to be a significant arbitrage opportunity over a fairly long time scale as the ask prices lower, perhaps in response to the volatile bid prices(which may be a result of traders from other areas eating up the available liquidity on the bid side), then rise again after the shock at t=50.
In this series, a liquidity shock occurs when x=50(although there are several shocks prior to this). The whole sequence from x=1 to x=50 takes place over 13 seconds, and each x value is a distinct trade or quote event. The red points are ask prices, and the blue points are bid prices. As you can see, there appears to be a significant arbitrage opportunity over a fairly long time scale as the ask prices lower, perhaps in response to the volatile bid prices(which may be a result of traders from other areas eating up the available liquidity on the bid side), then rise again after the shock at t=50.
This same pattern exists in other tick data time series that were given to competitors in this challenge, which could make for potentially interesting arbitrage opportunities if it is able to be exploited.
Another interesting feature of the tick data when plotted over time is the fact that there is much higher volatility earlier in the day. This corresponds with several papers that noted the same phenomenon. When training a predictive model on tick data, a significant portion of the days error(30-40%) can occur in the first hour of trading. This points to the need for specialized models to be developed for the first hour of trading, but it also points to the fact that the first hour, is, in some ways, relatively unpredictable. A model that does not attempt to make predictions in the first hour may make significantly more “correct” guesses and thus significantly more profit than one that does not.
The below plot is an easier way to look at this. It uses the tapply function to find the mean normalized residual for each one-minute time slice in the trading day:
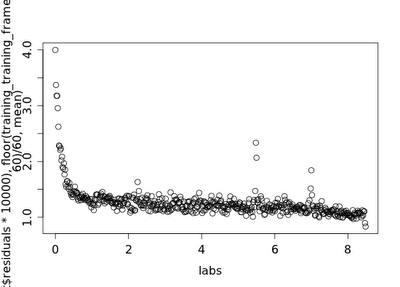 As you can see, there is more than 4 times as much prediction error(remember, a proxy for volatility) in the first minute as there is in the last.
As you can see, there is more than 4 times as much prediction error(remember, a proxy for volatility) in the first minute as there is in the last.
I will wrap this post up at this point. I will post more of my findings soon.
